○The universe is a four-dimensional space-time consisting of three-dimensional space and time, and the space-time can shrink or elongate. (Special relativity [1])
○ The speed of light(electromagnetic wave) traveling space-time is constant. (Special relativity)
○ You can write the relationship of energy and mass and speed of light with following equation. (Special relativity)
E=mc^2
※c^2:raise c to the 4 power
(E:energy(J)、m:mass(g)、c:speed of light(m/s))
○If the mass of the object which exercises reaches speed of light, it will become infinite. (Special relativity)
○The space-time is distorted. (General relativity[2])
○ The universe is expanding. (General relativity)
○ Black hole exists. (General relativity)
※ In accordance with Special relativity and General relativity, it is called Theory of relativity.
※ According to theory of relativity, the phenomenon in which an error becomes large if Newtonian mechanics describes (movement near the speed of light and movement in a big gravitational field) , can be described correctly.
【References】
1. Special relativity(1905)[Electromagnetic force ]
:The theory which dealt with the inertia system in the state where there is no gravity.
○The universe is the 4-dimensional world of time and space. The "space-time" seen from the watcher is a relative thing which is rectified by Lorentz transformation, and is extended or is shrunk.
○The length of a spacecraft is shrunk by a cross direction at a rate of.
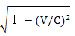
(V: Motion speed, C:Light speed)
○At the system which exercises, compared with an external system, only is delayed in time.
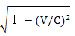
2. General relativity [Electromagnetic force + Gravity]
:Theory of gravity and space-time about the macro world such as the movement of the stars and the structure of the galaxy. (1915 - 1916)
• This theory described that gravity is generated by distortion of spacetime by mass.
・It is the extended equation of the Newton's law of universal gravitation, so that it can be applied to the strong gravitational field . By substituting the material and energy density such as a star on the right side, it is possible to estimate the curvature of the space-time around the star.
・Genera relativity can properly describe phenomenon(ex. exercise close to light-speed, or movement in a large gravitational field of such a black hole) more than Newtonian mechanics.
・Generally relativity predicts that black hole is formed where large mass is concentrated in a limited space.
○ Einstein’s equation: If you assign the mass of the material such as a star or energy in the right-hand side, it is possible to calculate the curvature of space-time around the star.
Gμν+Λgμν=κTμν
※ Left-hand side: Curvature of space-time (Geometrical quantity representing the bending of space-time):Total energy of the galaxy
※ Right-hand side: Density of matter and energy (causing a gravity) that exist in the universe
⇒In the flat universe of curvature zero, the total energy for the entire galaxy becomes zero.
=In the flat universe, the sum of the negative energy due to gravity (repulsion) and the positive energy(kinetic energy) is zero.
・Gμν:Einstein tensor(Tensor represents the distortion)
・Λgμν : The cosmological constant
・κ :Einstein's constant of gravitation
(κ=8πG/c^4 (π:pi、G:Gravitational constant、c :Speed of light))
※c^4:raise c to the 4 power
・Tμν:energy-momentum tensor
・μ, ν: Identify the coordinates of space-time.
○As astronomical phenomena were discovered, such as the 3-kelvin microwave background radiation (1965), pulsars (1967), and the first black hole candidates (1981), General relativity explained their attributes, and measurement of them further confirmed the theory.
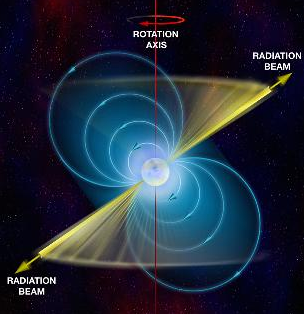
※Image of pulsar [2]
【Referendes】
1. Theory of relativity - Wikipedia
2. Dave Finley “Pulsars: The Universe's Gift to Physics”at National Radio Astronomy Observatory 20120219
https://www.nrao.edu/pr/2012/aaaspulsars/
【Change log】
20170430 Addition of figure etc.
0 件のコメント:
コメントを投稿