○量子もつれ(エンタングルメント)のエントロピー:量子もつれの数。量子もつれの定量化の指標。=EPR対(EPR:Einstein-Podolsky-Rosen)の数
○場の量子論で量子もつれのエントロピーを計算しようとすると非常に難しいが、反ド・ジッター空間では、ホログラフィックにバブル(表面積が最小になるようなブラックホールのような形状のもの)の表面積の計算に置き換えることができる。:笠・高柳公式(Holographic Entanglement Entropy Formula 2006)[1]
※反ドジッター空間/AdS: Anti de Sitter 時空:曲率が負で一定の空間(の一つ)
=負の宇宙定数Λ(暗黒エネルギー)を持つ宇宙
⇔dS: de Sitter 空間(曲率:正)[2]
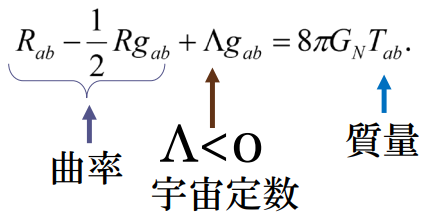
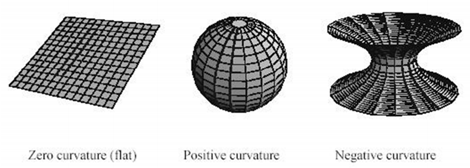
図:曲率 [3]
・AdS 空間の大きな特徴は無限大の空間を、有限の領域に包み込めること。

図:エッシャーの絵:反ド・ジッター空間を平面に投影したイメージに近い。
・現実の宇宙に近いのはド・ジッター空間(Λ>0)だが、そのホログラフィック原理は解明されていない。[4]
○笠-高柳(Ryu-Takayanagi)公式(2006 年):量子もつれのエントロピーのホログラフィー公式
・量子もつれとホログラフィック原理が関係していることを明らかにした。
・場の量子論での量子のもつれのエントロピーの計算は、反ド・ジッター空間に発生したバブル(表面積が最小になるような形状のもの)の表面積の計算に置き換えることができる。[5] [6]

図:境界面から AdS 空間の内部に伸びていく極小局面を考え、その面積を計算して重力理論のニュートン定数の4倍で割ったものが、エンタングルメント・エントロピーに 等しい。
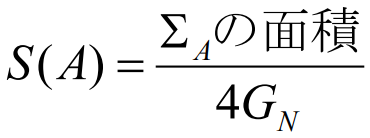
※笠-高柳公式
・ベッケンシュタイン-ホーキングのブラック ホール・エントロピー公式の一般化。
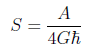
※ベッケンシュタイン-ホーキングの公式 [7]
○笠-高柳公式では、プランク面積(1平方プランク長)あたり1ビットの量子もつれが存在することになる。
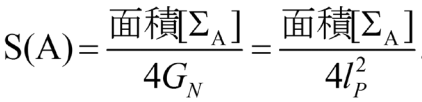
※プランク長

○課題:ド・ジッター宇宙と量子もつれについて解明する必要がある。[8]
○量子もつれのエントロピーの応用:
・ブラックホールの形成、特異点などの様々な(量子)重力現象の理解に役立つ。[9]
・ある種の物質では原子間距離と温度を制御すると、通常の金属とは電気特性(超電導)が異なる「ストレンジメタル(異常金属anomalous metallic phase)」に転移するが、これは物質を構成する電子が全体として量子もつれ状態になること(量子もつれのエントロピーの急増)によって生じる。
※異常金属:超伝導転移温度より高温で抵抗率が温度に比例する銅酸化物超伝導体高温超伝導体)などがその例。[10]
【参 照】
1. 中島林彦“ホログラフィー原理を解く“at 日経サイエンス 201701
2. 高柳 匡"超ひも理論の最前線:宇宙は量子ビットから創られているのか?“ 20170524
3. 中村 真“非専門家のためのAdS/CFT対応入門” 20111214
4. 高柳 匡"超ひも理論の最前線:宇宙は量子ビットから創られているのか?“ 20170524
5. J. マルダセナ「重力は幻なのか?」日経サイエンス200602
6.中島林彦“ホログラフィー原理を解く“at 日経サイエンス 201701
7.No.29-2 熱力学とニュートンの法則
8.高柳 匡"超ひも理論の最前線:宇宙は量子ビットから創られているのか?“ 20170524
9.Tadashi Takayanagi “Entanglement Entropy and AdS/CFT” 2012
10.異常金属
https://pub.maruzen.co.jp/book_magazine/magazine/parity-back/parity2011/2011_12/1112_key.html
【履 歴】
20180117 新規
0 件のコメント:
コメントを投稿