18-1 Uncertainty principle
Introduced first in 1927, by the German physicist Werner Heisenberg, it states that the more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa.
You can answer only according to probability on the level of quantum.
○The formal inequality relating the standard deviation of position σx and the standard deviation of momentum σp
σxσp≧h
:No matter how improve the accuracy of the measurement, the product of the standard deviation of the position and momentum is greater than h.
:One is uncertain when you try to confirm the other.
・x:position、p:momentum
・h:Planck constant(6.626×10^-34 J・s)
○In the case of energy and time
σEσt≧h
:Beating only a little law of conservation of energy, it may be borrowed energy.
※However it must return as fast as borrow a lot.
・E:energy、t: time
⇒Energy is possible to materialize.⇒Pairs of matter and anti-matter particles are constantly being created and annihilated.
=Quantum fluctuations
⇒Also in vacuum, pairs of matter and anti-matter particles are constantly being created and annihilated.: Vacuum fluctuations
⇒The vacuum has a vastly complex structure.
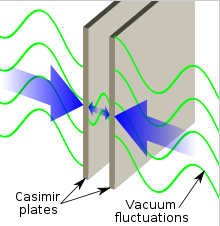
・Vacuum fluctuations causes a measurable force (Casimir effect) in infinitesimal.

※Vacuum fluctuations [3]
18-2 Casimir effect
○The typical example is of the two uncharged conductive plates in a vacuum, placed a few nanometers apart. The Casimir effect produces the negative pressure. It is due to quantum vacuum fluctuations of the electromagnetic field.
○As the two mirrors move closer to each other, the longer waves will no longer fit--the result being that the total amount of energy in the vacuum between the plates will be a bit less than the amount elsewhere in the vacuum. Thus, the mirrors will attract each other, just as two objects held together by a stretched spring will move together as the energy stored in the spring decreases. [4]
・The dynamical Casimir effect is the production of particles and energy from an accelerated moving mirror. [5] Further, there may help development of quantum computers.
18-3 Phase Transitions of Vacuum /Inflation Cosmology/Quantum Tunneling
○Vacuum is to shift to more of the state of low energy:phase transition.
○In physical cosmology, cosmic inflation, cosmological inflation, or just inflation is a theory of exponential expansion of space in the early universe. The inflationary epoch lasted from 10 minus 36 square seconds until after 10 minus 34 square seconds.
(The size of the universe (10^-27m) is much smaller than atom (10^-10m).
⇒3 millimeters (10^-3m))
○The driving force behind this inflation has been said that the energy that was released during the phase transition of the vacuum.
○In early inflationary models, the phase transition of the vacuum was considered that it is generated by the Quantum tunnelling or tunnel effect. However, in a model named new inflation or slow-roll inflation, instead of tunneling out of a false vacuum state, inflation is considered that occurred by rolling down a potential energy hill.
※Quantum tunnelling or tunnel effect to the quantum mechanical phenomenon where a particle tunnels through a barrier that it classicallycould not surmount. In the quantum theory it is explained by the uncertainty principle.
It has important applications to modern devices such as the tunnel diode, quantum computing, and the scanning tunnelling microscope. [3]
【Refereces】
1.Wikipedia: Uncertainty principle
2. ハイゼンベルクの不確定性原理 - nifty Uncertainty principle- nifty
http://homepage2.nifty.com/einstein/contents/relativity/contents/relativity3055.html
3.RevoScience”Young researcher proposes new explaination for unsolved problems in physics…”
http://revoscience.com/en/young-researcher-proposes-new-explaination-for-unsolved-problems-in-physics-and-revolutionizes-the-theory-of-quantum-fluctuations/
4. “What is the Casimir effect?”SCUENTIFIC AMERICAN 1998
http://www.scientificamerican.com/article/what-is-the-casimir-effec/
5. Wikipedia:Casimir effect
0 件のコメント:
コメントを投稿