１７ 量子力学

１７　量子力学　【宇宙とは】宇宙との対話

１７－１　量子力学とは？ [1]
○語源：エネルギー、長さ、速度、時間などの物理量には、それ以上分割できない最小単位（量子）がある。

○電子（：2.8×10^－15ｍ）程度の大きさの粒子（物質）は波動方程式（シュレディンガー方程式：偏微分方程式 1926）を解いて波動関数を得るか、ハイゼンベルクの運動方程式（行列式 1925）を解くとその状態（エネルギーの値）が分かる。
：波動関数を微分するとエネルギーや運動量の値が分かる。
※波動方程式とハイゼンベルクの運動方程式は数学的に等価。

○波動方程式
・量子力学の基本方程式。古典力学のニュートンの運動方程式と対比される。
・物質波の状態を確率的に計算することが出来る。
・波動方程式は古典力学や数学から厳密に導けるものではない。現象を上手く説明する方程式。
※相対論は古典力学

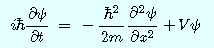
：換算プランク定数（エイチバー）
ｔ：時間
ｍ：粒子の質量
Ψ（プサイ）：波動関数（wave function）：波動を表すために導入した複素量
X：位置
V：ポテンシャルエネルギー

○波動関数の２乗は粒子の存在確率。
・下図は物質の存在確率とエネルギー状態のグラフ。[2]

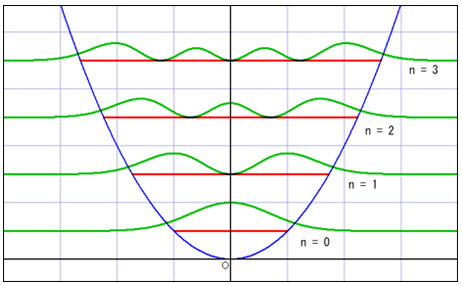
※赤色の線はエネルギーの状態(n)で、存在確率とｎは飛び飛びに変化する。
※ニュートン力学の場合にはその赤線が示す幅の内側で粒子が振動するが、量子力学的な存在確率の波はその範囲を越えて広がっている。

○古典力学は量子力学の近似にすぎない。たまたま量子力学的現象が顕著でないような場合に限って古典力学を使ってもかまわない。[3]

☆宇宙は、エネルギーが数学的な規則に従うことで、全く同じ性質を持った粒子を限りなく持つ！ 

○量子論的な真空のゆらぎにより宇宙が誕生した。

○波動方程式が複素数を含むので波動関数は複素数の関数。
・・・宇宙は虚数によって表現される！ [4]

１７－２　物質波（ド・ブロイ波（de Broglie wave））の理論
○極微のレベルでは粒子と波との間に厳密な境界はない。
→波動として存在をとらえたとき、物理学ではそれを「場」と呼ぶ。たとえば光は電場と磁場の波動である。

※波としての性質が実際に観測されるのは、電子線のような極めて微視的な状況下。
※電子は波で（その大きさを求めることは不可能）、原子核における電子の軌道の長さは波長（１０のマイナス１０乗ｍ）の整数倍。
＝電子が原子核に落ち込まない理由

○複素数の波のイメージ [2]

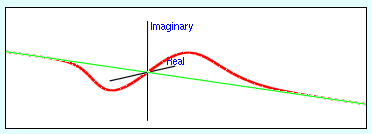
※波全体が１個の粒子を表す。
※波の高さや深さは波動関数の大きさに相当する。：ド・ブロイ波＝波動関数

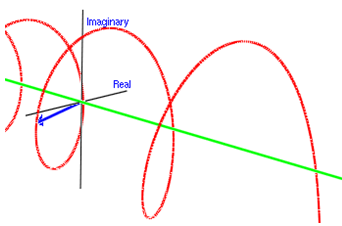
○物質波：複素数で表される空間を動く波 [5] ：方向の無いスカラー波

　　
１７－３　量子力学の成果 [6]
・原子内部の運動の説明
・化学反応（共有結合）を計算で説明
・反物質、負のエネルギーの存在説明
・半導体工学の基礎理論　→　電子機器の設計
（レーザー、トランジスタ（マイクロチップ）、電子顕微鏡、MRI、発光ダイオード、USBメモリ）
・超電導、超流動の基礎理論
・量子暗号
・量子コンピュータの開発
・量子テレポーテーション
・並行宇宙論

○課題
・量子力学と一般相対性理論を合わせた理論（量子重力理論）は、いまだ完成されていない。

１７－４　不確定性原理　→　Ｎｏ．１８

【参　照】
1.五十嵐靖則“量子論の世界がわかる”
https://books.google.co.jp/books?id=rJwmaVXTRRgC&pg=PA104&lpg=PA104&dq=%E8%A4%87%E7%B4%A0%E6%95%B0%E3%81%AE%E6%B3%A2%E3%81%AE%E3%82%A4%E3%83%A1%E3%83%BC%E3%82%B8&source=bl&ots=6DM1n4CVte&sig=Kjo5ljS7cub5_e8NKjOKj7CISrY&hl=ja&sa=X&ved=0ahUKEwiZ0978pdzOAhWGFJQKHd60AUUQ6AEIOTAM#v=onepage&q=%E8%A4%87%E7%B4%A0%E6%95%B0%E3%81%AE%E6%B3%A2%E3%81%AE%E3%82%A4%E3%83%A1%E3%83%BC%E3%82%B8&f=false
2.広江　克彦”EMANの量子力学”
http://eman-physics.net/quantum/contents.html
3. 量子力学 - Wikipedia
4.虚数は私たちの世界観を変えてしまった。 - とね日記
http://blog.goo.ne.jp/ktonegaw/e/ed35400df27a2bc7e597531c08d99869
5. EMAMの物理学・量子力学／調和振動子
http://eman-physics.net/quantum/oscillator.html
6. Quantum mechanics - Wikipedia