○宇宙は3次元の空間と時間という4次元の時空であり、空間と時間は伸びたり縮んだりする。(特殊相対性理論)
○時空を移動する光(電磁波)の速さは一定である。(特殊相対性理論)
○エネルギーと質量と光速の関係は次の式で書ける。
E=mc^2
※c^2:cの2乗
(E:エネルギー(J)、m:質量(g)、c:光の速度(m/s))
○運動する物体の質量は光速に達すると無限大になる。(特殊相対性理論)
○時空は歪んでいる。(一般相対性理論)
○宇宙は膨張している。(一般相対性理論)
○ブラックホールが存在する。(一般相対性理論)
※特殊相対性理論と一般相対性理論の2つの理論をあわせて相対性理論と呼ばれる。
※相対性理論では、ニュートン力学で記述すると誤差が大きくなる現象(光速度に近い運動や、大きな重力場における運動)を正しく記述できる。
【参 考】
1.特殊相対性理論(1905年)[電磁気力]
:電磁気学の理論。重力のない状態での慣性系を取り扱っている。
○観測者から見た「時空」は、ローレンツ変換により補正され、伸びたり縮んだりする相対的なもの。
○宇宙船の長さは前後方向に
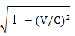
の割合で縮む。
(V:運動する速度、C:光の速度)
○運動する系では、外部の系に比べて
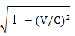
だけ時間の進み方が遅れる。
2. 一般相対性理論(1915 - 1916年)[電磁気力+重力]
:星の運動や銀河系の構造などマクロな世界の重力と時空の理論。
・質量が時空間を歪ませることによって、重力が生じることを説明した。
・ニュートンが導いた万有引力の法則を、強い重力場に対して適用できるように拡張した方程式であり、星のような物質とエネルギーの密度を右辺に代入すれば、その星の周りの時空がどういう風に曲がっているかを推定することができる。
・ニュートン力学で記述すると誤差が大きくなる現象(光速度に近い運動や、ブラックホールなどの大きな重力場における運動)を正しく記述できる。
・限られた空間に大きな質量が集中すると、ブラックホールが形成されることを予測した。
○アインシュタイン方程式(重力場の方程式)を使うと、星のような物質またはエネルギーを右辺に代入すれば、その星の周りの時空がどういう風に曲がっているかを読みとることができる。
Gμν+Λgμν=κTμν
※左辺は時空の曲率(時空の曲がり具合):銀河の全エネルギー
※右辺は宇宙に存在する物質とエネルギー(重力を生じさせるもの)の密度
⇒曲率ゼロの平坦な宇宙では、全銀河についての全エネルギーは、ゼロになる。
=平坦な宇宙では、運動が持つ正のエネルギーと重力(斥力)による負のエネルギーとの和はゼロになる。
・ Gμν:アインシュタイン・テンソル(テンソルとは歪みを表すもの。)
・Λ :宇宙定数。この項は宇宙項と呼ばれる。
アインシュタインは1917年に定常な宇宙を導くため、重力場方程式に宇宙項(:万有斥力)を加えた。
・κ :アインシュタインの重力定数。
( κ=8πG/c^4 の関係にある(π は円周率、Gは万有引力定数、c は光速))
※c^4:cの4乗(raise c to the 4 power)
・ Tμν:エネルギー・運動量テンソル。
・ 添え字μ,νは、それぞれ時空の座標を特定するもの。
○一般相対性理論は、1960年代のマイクロ波背景放射(1965)、高速回転する中性子性のパルサー(1967)、最初のブラックホール候補(1981)などの発見により確証された。
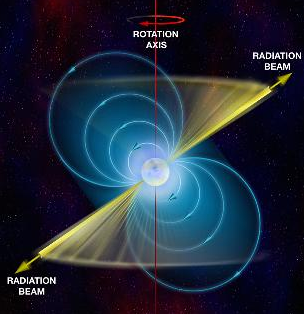
※Image of pulsar [2]
【参 照】
1. Theory of relativity - Wikipedia
2. Dave Finley “Pulsars: The Universe's Gift to Physics”at National Radio Astronomy Observatory 20120219
https://www.nrao.edu/pr/2012/aaaspulsars/
【更新履歴】
20170430 図などの追加
0 件のコメント:
コメントを投稿